앞장에서 word2vec의 구조를 배우고 CBOW모델을 구현했다. 단순한 2층 신경망이라서 간단하게 구현할 수 있었다.
이 구현에는 몇가지 문제가 있다. 가장 큰 문제는 말뭉치에 포함된 어휘수가 많아지면 계산량이 커져 계산 시간이 너무 오래걸린다.
이러한 점 때문에 이번 장의 목표는 word2vec의 속도 개선으로 잡아보았다.
첫번째 개선은 Embedding이라는 새로운 계층을 도입한다. 두번째로는 네거티브 샘플링이라는 새로운 손실 함수를 도입한다.
이 두가지 개선으로 PTB 데이터셋(실용적인 크기의 말뭉치)을 가지고 학습을 수행할 것이다.
word2vec 개선 1 - Embedding
앞장에서 CBOW 모델 구현 복습을 해보자.
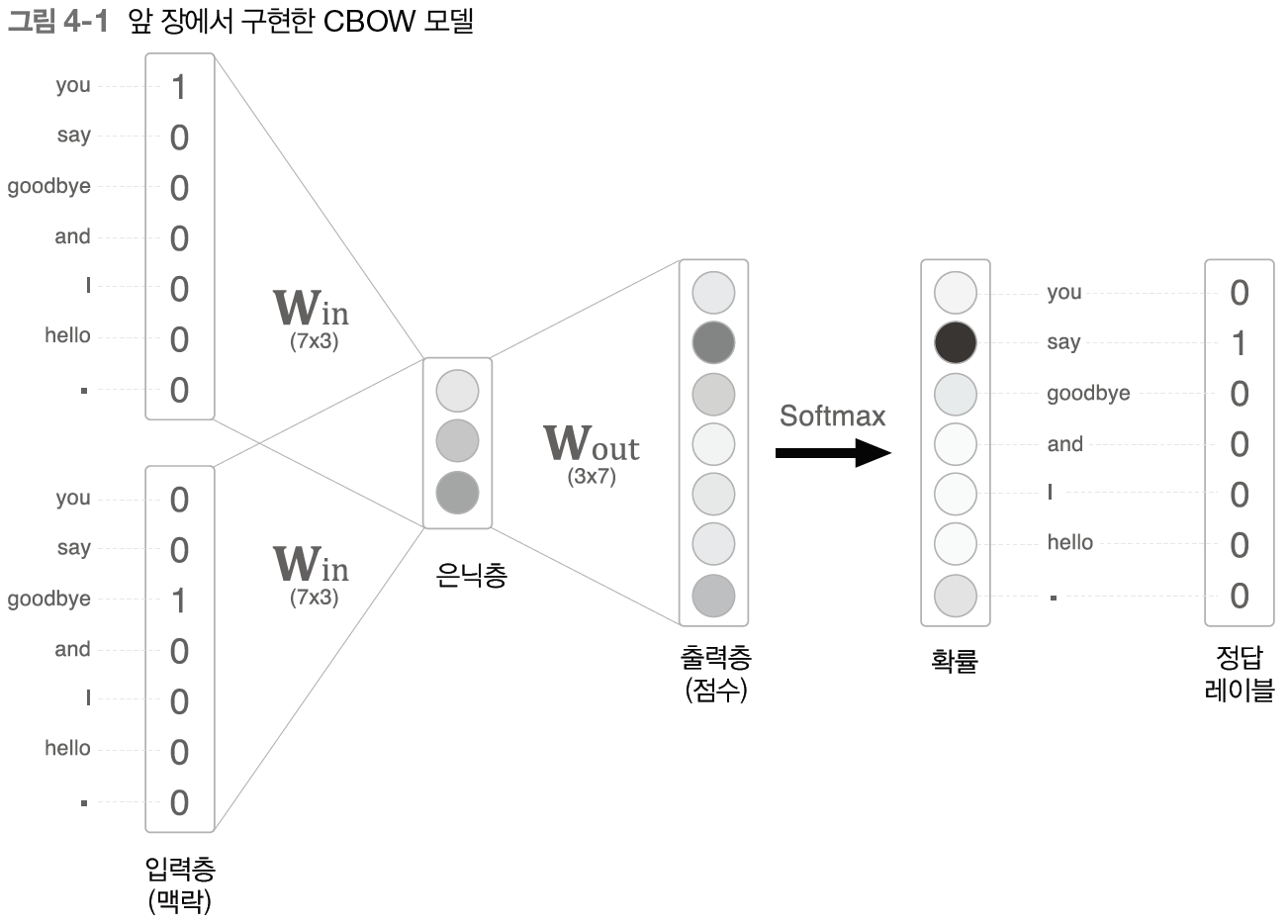
단어 2개를 contexts로 사용해, 하나의target을 추측한다.
이때 가중치 Win과의 행렬 곱으로 은닉층이 계산되고, Wout와의 행렬 곱으로 각 단어의 점수를 구한다.
이후 Softmax함수를 적용해 각 단어의 출현 확률을 얻고, 이 확률을 교차 엔트로피 오차를 적용하여 손실을 구한다.
위의 모델에서 거대한 말뭉치를 다루게 되면 문제가 발생한다.
어휘가 100만개, 은닉층 뉴런이 100개인 CBOW 모델을 가정해보자. 그러면 word2vec은 다음 그림처럼 된다.

그림에서 보듯, 입력층과 출력층의 수많은 뉴런 때문에 중간 계산에 많은 시간이 소요된다.
정확히는 다음의 두 계산이 병목이 된다.
- 입력층의 원핫 표현과 가중치 행렬 Win의 곱 계산
- 은닉층과 가중치 행렬 Wout의 곱 및 Softmax 계층의 계산
두 병목을 해소할 수 있도록 Emdedding 계층 도입, 네거티브 샘플링(손실 함수)을 도입해 해결해보자.
Embedding 계층
앞장의 word2vec에서는 단어를 원핫 표현으로 변경했다.
이것을 MatMul계층에 입력하고, MatMul계층에서 가중치 행렬을 곱햇다.
어휘 수가 100만개, 은닉층 뉴런이 100개라면, MatMul계층의 행렬 곱은 다음 그림처럼 된다.

그림에서 결과적으로 수행하는 일은 단지 행렬의 특정 행을 추출하는 것 뿐이다.
사실상 원핫 표현으로의 변환과, MatMul계층의 행렬 곱 계산은 필요가 없는 것이다.
그러면 가중치 매개변수로부터 단어 ID에 해당하는 행(벡터)을 추출하는 계층을 Embedding계층이라고 부르자.
Embedding 계층에 단어 임베딩(분산 표현)을 저장하는 것이다.
Embedding 계층 구현
행렬에서 특정 행을 출력하는 것은 쉽다.
가중치 W가 2차원 numpy matrix일때, 이 가중치로부터 특정 행을 추출하려면 원하는 행을 명시하면 된다.
코드는 다음과 같다.
import numpy as np
W = np.arange(21).reshape(7, 3)
print(W)
print(W[2])
print(W[5])
또한, 가중치 W로부터 여러 행을 한꺼번에 추출하는 일도 간단하게 할 수 있다.
다음 코드를 보자.
idx = np.array([1,0,3,0])
print(W[idx])
인덱스 4개를 한번에 추출하였다. 이는 미니배치 처리를 가정했을 경우의 구현이다.
Embedding계층의 forward 구현 코드를 보자.
class Embedding:
def __init__(self,W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.idx = None
def forward(self,idx):
W, = self.params
self.idx = idx
out = W[idx]
return outidx에는 추출하는 행의 인덱스(단어 ID)를 배열로 저장한다.
이어서 backward의 경우를 생각해보자. Embedding계층의 순전파는 가중치 W의 특정 행을 추출할 뿐이였다.
따라서 역전파에서는 앞 층(출력 측 층)으로부터 전해진 기울기를 다음 층(입력 측 층)으로 그대로 흘려주면 된다.
다만, 앞 층으로부터 전해진 기울기를 가중치 기울기 dW의 특정 행(idx번째 행)에 설정한다.
그림으로 표현하면 다음과 같다.

backward의 코드 구현은 다음과 같다.
def backward(self,dout):
dW, = self.grads
dW[...] = 0
dW[self.idx] = dout
return None가중치 기울기 dW를 꺼낸 다음, dW의 원소를 0으로 덮어씌운다.
이후 앞층에서 전해진 기울기 dout을 idx인덱스에 저장한다.
사실 위의 backward 구현에는 문제가 하나 있다.
idx의 원소가 중복될 때 발생한다. idx가 [0, 2, 0, 4]일 경우를 생각해보자. 그럼 다음 그림과 같이 문제가 발생한다.
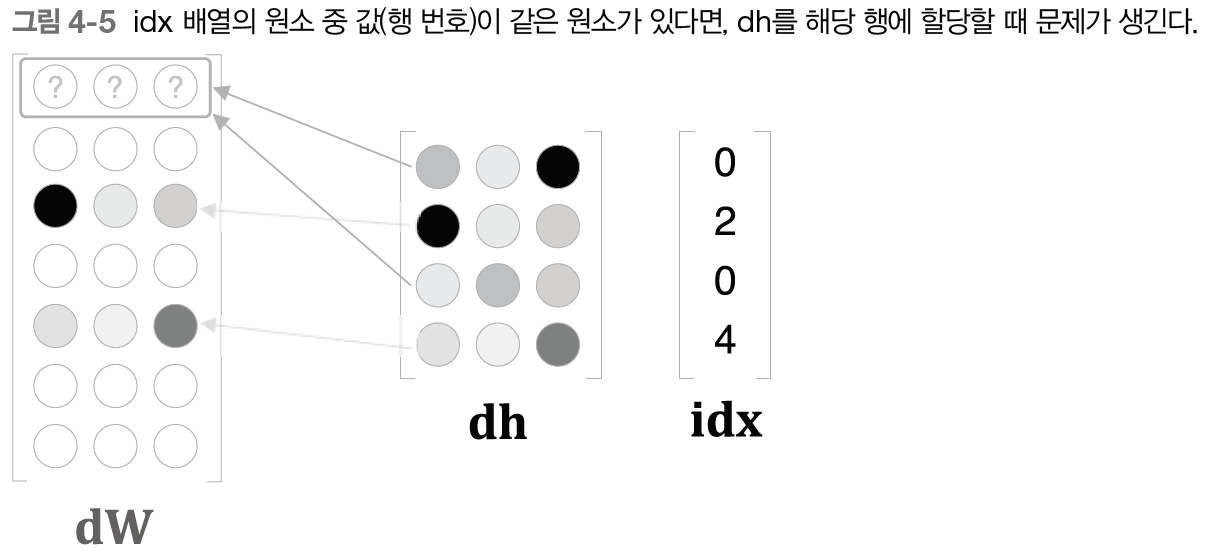
dW의 0번째 인덱스(idx = 0)인 경우 값이 덮어쓰기가 된다.
이 중복 문제를 해결하려면 할당이 아닌 더하기를 수행하여야 한다.
dh의 각 행의 값을 dW의 해당 행에 더해준다.
그 이유는,
- 동일한 임베딩 벡터(행)을 여러번 참조한 경우, 각 연산에서 발생한 기울기를 모두 더해야 한다.
- 역전파 기울기의 합산 규칙 - 연쇄 법칙에 기반하며 손실 함수에 특정 변수가 여러 경로를 통해 기여할 경우, 모든 경로에서 전달된 기울기를 합산하여야 한다.
그럼 수정된 역전파의 코드를 보자.
def backward(self,dout):
dW, = self.grads
dW[...] = 0
for i, word_id in enumerate(self.idx):
dW[word_id] += dout[i]
#혹은
# np.add.at(dW,self.idx,dout)
return Nonenp.add.at(A,idx,B)는 B를 A의 idx번째 행에 더해준다.
일반적으로 파이썬에서 for문보다 numpy의 내장 메서드를 사용하는 편이 더 빠르다.
numpy의 메서드에는 속도와 효율을 높여주는 최적화가 적용되어 있기 때문이다.
이상으로 이 Embedding 계층은 입력측 MatMul계층 자리에 전환할 수 있다.
메모리 사용량을 줄이고 쓸데없는 계산도 생략할 수 있다.
word2vec 개선 2 - 네거티브 샘플링
두번째 개선은, 은닉층 이후의 처리(행렬 곱과 Softmax의 계산) 부분의 개선이다.
네거티브 샘플링을 이용해 개선한다. Softmax대신 네거티브 샘플링을 사용하면 계산량을 일정하게 억제할 수 있다.
은닉층 이후 계산의 문제점
문제점을 알아보기 위해 어휘가 100만개, 은닉층 뉴런이 100개일 때의 word2vec(CBOW 모델)을 예로 생각해보자.

Softmax에서의 수식을 보면, 계산량이 매우 증가하는 것을 볼 수 있다.

k번째 원소(단어)를 타깃으로 했을 때 Softmax의 계산식이다. (점수의 각 원소는 s1,s2,...)
계산이 어휘 수에 비례해 증가하므로 Softmax를 대신할 가벼운 계산이 필요하다.
다중 분류에서 이진 분류로
네거티브 샘플링의 핵심 아이디어는 이진 분류(binary classification)이다.
더 정확하게 말하면, 다중 분류(multi classification 혹은 다중 클래스 분류)를 이진 분류로 근사하는 것이 네거티브 샘플링을 이해하는데 중요한 포인트이다.
지금까지 우리는 다중 분류 문제를 다뤄왔다. 앞절의 예도 100만개의 단어 중에서 옳은 단어 하나를 선택하는 문제였다.
그렇다면 이러한 문제를 이진 문제로 다룰 수 있을까?
정확히는 다중 분류 문제를 이진 문제로 근사할 수 없을까?
이진 분류는 Yes/No로 답하는 문제를 다룬다. 예를 들어 'target은 say입니까?' 처럼.
지금까지는 맥락이 주어졌을 때 정답이 되는 단어를 높은 확률로 추측하도록 만드는 일을 했다.
학습이 잘 이뤄지면, 올바른 추측을 수행하게 된다.
이제부터 해결해야 할 점은 다중 분류 방식을 이진 분류 방식으로 해결하는 것이다.
"contexts가 you와 goodbye일 때, target은 say인가?" 라는 질문에 답하는 신경망을 생각해내야 한다.
이렇게 되면 출력층에는 뉴런을 하나만 준비하면 된다. 출력층의 뉴런이 say의 점수를 출력하는 것이다.
CBOW 모델의 그림을 보자.

은닉층과 출력 측의 가중치 행렬의 내적은 say에 해당하는 열(단어 벡터)만을 추출하고, 추출된 벡터와 은닉층 뉴런과의 내적을 계산하면 끝이다.
계산을 자세히 하면 다음과 같다.
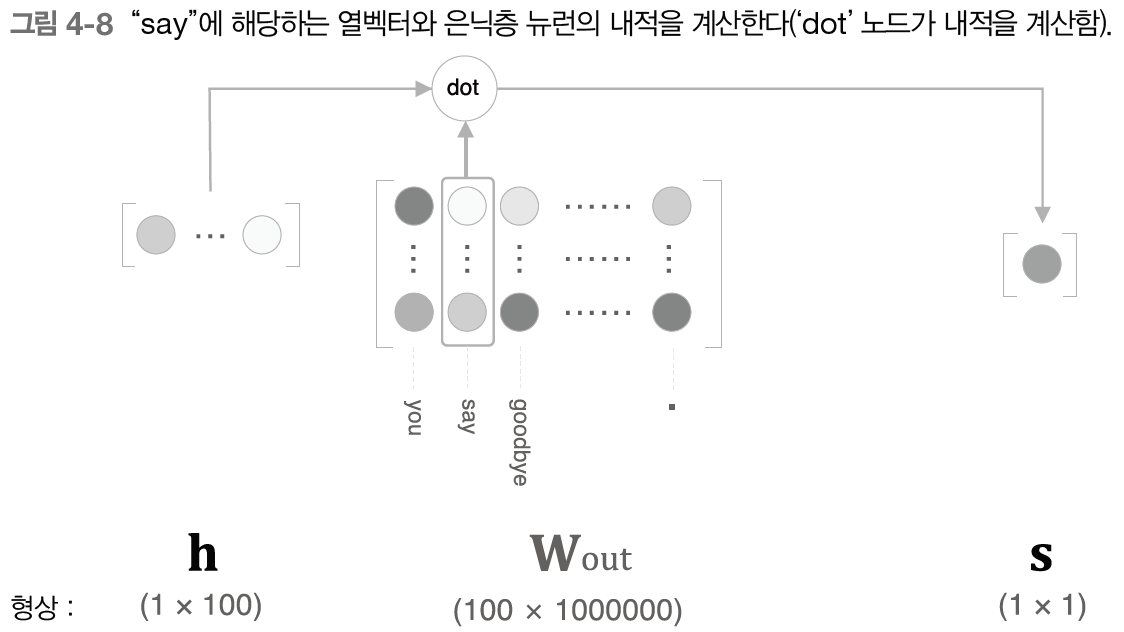
그림처럼 Wout에는 각 단어 ID의 단어 벡터가 열로 저장되어 있다.
이 예에서는 say에 해당하는 단어 벡터를 추출한다. 그 후 벡터와 은닉층 뉴런과의 내적을 구한다.
이렇게 구한 값이 최종 점수가 된다.
이전까지의 출력층은 모든 단어를 대상으로 계산을 수행했다.
하지만 여기에서는 단어 하나에 주목하여 그 점수만을 계산하는 것이 차이점이다.
sigmoid함수를 사용해 이 점수를 확률로 변환한다.
시그모이드 함수와 교차 엔트로피 오차
다중 분류의 경우, 출력층에서 점수를 확률로 변환할 때 Softmax함수를, 손실 함수로는 Cross Entropy를 사용한다.
이진 분류의 경우, 출력층에서는 Sigmoid를, 손실 함수로는 Cross Entropy를 이용한다.
시그모이드를 잠깐 복습해보자. 수식은 다음과 같다.

위 식을 그래프로 그리면 아래와 같다.

그래프는 S자 곡선 형태이며, 입력값 x는 0에서 1 사이의 실수로 변환된다.
여기서 핵심은 출력 y를 확률로 해석할 수 있다.
시그모이드를 통해 y를 얻으면, 교차 엔트로피 오차를 이용해 손실을 구한다.
교차 엔트로피 오차의 수식은 다음과 같다.

y는 시그모이드 함수의 출력, t는 정답 레이블(원-핫 코딩)이다.
따라서 t가 1(정답)이면 -logy가 출력되고, 0이면 -log(1-y)가 출력된다.
이어서 Sigmoid와 Cross Entropy Error 계층의 계산 그래프를 살펴보자.

위 그림에서 주목할 점은 역전파의 y - t 값이다. (dL/dx가 y-t로 유도되는 식은 생략)
t가 1(정답)이라면 y가 1(100%)에 가까워질수록 오차가 줄어든다. 반대로 y가 1에서 멀어지면 오차가 커진다.
이 오차가 앞 계층으로 흘러가므로, 오차가 크면 크게 학습하고, 오차가 작으면 작게 학습하게 된다.
다중 분류에서 이진 분류로 (구현)
구현 관점에서 정리해보자.
다중 분류에서는 출력층에 어휘 수만큼 뉴런을 준비하고 출력한 값을 Softmax계층에 통과시켰다.
이때 이용되는 신경망을 계층과 연산 중심으로 그리면 다음과 같다.

contexts가 you와 goodbye, target은 say인 경우의 예이다.
입력층에서는 각각에 대응하는 단어 ID의 분산 표현을 추출하기 위해 Embedding 계층을 사용했다.
위 그림은 이진 분류 신경망으로 변환해보자. 신경망 구성을 보면 다음 그림과 같다.
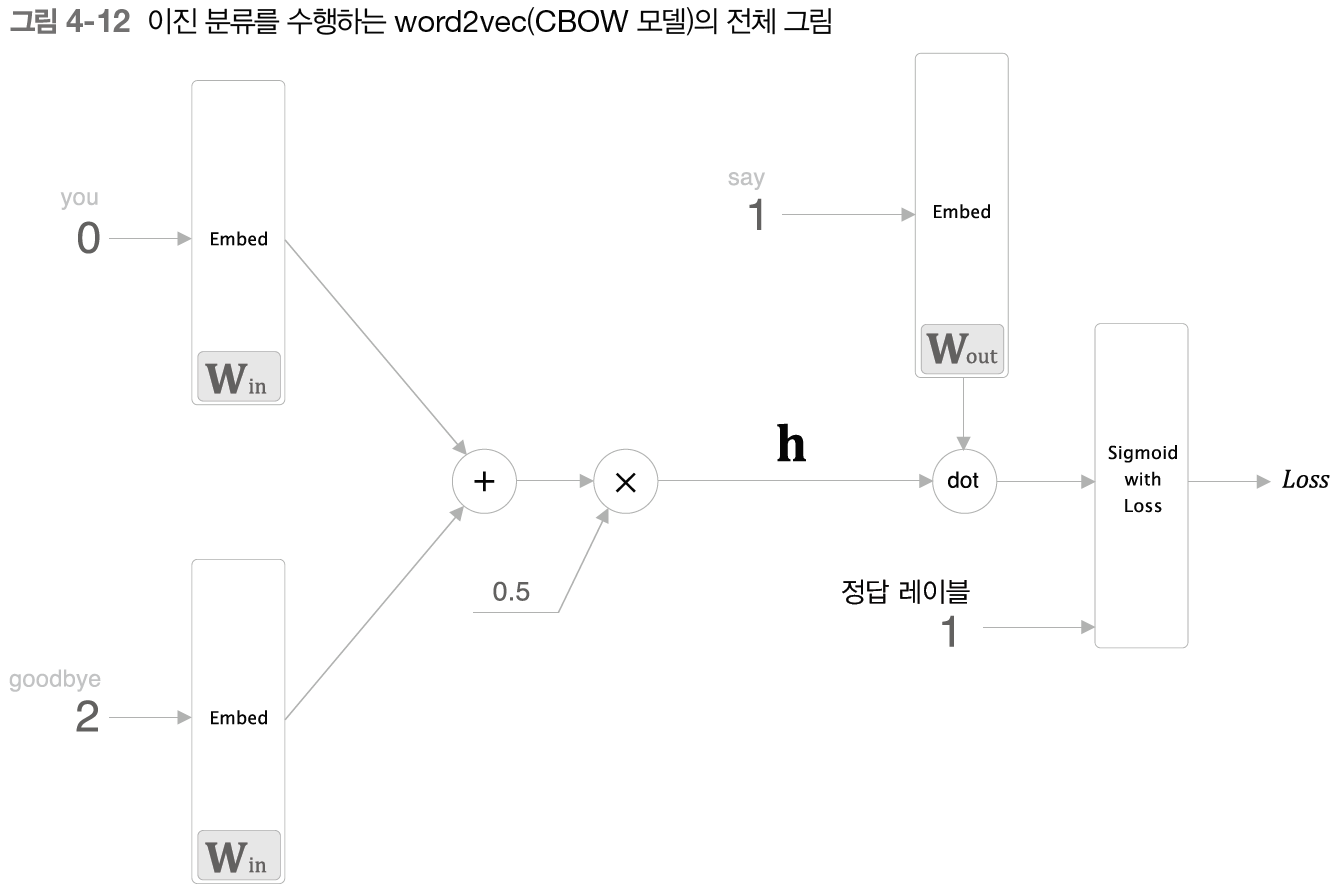
은닉층 h와 Wout에서 say에 해당하는 단어 벡터와의 내적을 계산하고 Sigmoid with Loss에 입력해 최종 손실을 얻는다.
후반부 계산을 좀 더 단순하게 만들면 Embedding 계층과 dot(내적)의 처리를 합친 계층을 만들 수 있다.
다음 그림을 참고하자.

은닉층 뉴런 h는 Embedding Dot 계층을 거쳐 Sigmoid with Loss 계층을 통과한다.
Embedding Dot 계층의 구현을 간단히 살펴보자.
# -*- coding: utf-8 -*-
"""
Created on Tue Dec 24 14:02:45 2024
Created by SeungKeon Lee
"""
import numpy as np
import sys
sys.path.append('..')
from common.layers import Embedding
W = np.arange(21).reshape(7, 3)
idx = np.array([0, 3, 1])
num = np.array([0,3,0])
target_W = np.array(W[num])
h = np.arange(9).reshape(3,3)
class EmbeddingDot:
def __init__(self,W):
self.embed = Embedding(W)
self.params = self.embed.params
self.grads = self.embed.grads
self.cache = None
def forward(self,h,idx):
target_W = self.embed.forward(idx)
out = np.sum(target_W * h, axis = 1)
self.cache = (h,target_W)
return out
def backward(self,dout):
h, target_W = self.cache
dout = dout.reshape(dout.shape[0], 1)
dtarget_W = dout * h
self.embed.backward(dtarget_W)
dh = dout * target_W
return dh이 책의 규칙대로 매개변수,기울기를 저장하고 embed는 embedding계층을, cache는 순전파 시 계산 결과를잠시 유지하기 위한 변수로 사용한다.
forward(h, idx)는 은닉층 뉴런 h와 단어 ID의 numpy matrix인 idx를 받는다.
idx는 단어 ID의 배열인데, 배열로 받는 이유는 미니배치 처리를 가정했기 때문이다.
그 다음 Embedding계층의 forward(idx)를 호출한 다음 내적을 계산한다.
내적 계산은 np.sum(target_W * h, axis = 1)이다. 아래 예를 참고하자.

네거티브 샘플링
앞에서 구현한 내용은 정답에 대해서 학습했다.
오답을 입력하면 어떤 결과가 나올지 확실하지 않다.
일단 정답에 대해 계산 그래프로는 다음처럼 그릴 수 있다.

여기에선 say 이외의 단어에 대해서는 어떠한 지식도 획득하지 못하였다.
긍정적 예에 대해서는 Sigmoid의 출력을 1에 가깝게 만들고, 부정적 예(정답 이외의 단어)에 대해서는 Sigmoid의 출력을 0에 가깝게 만드는 것이다. 그림으로는 다음과 같다.

이런 결과를 만들어주는 가중치가 필요하다.
그러면 모든 부정적 예를 대상으로 이진 분류를 학습시키면 어떨까? 대답은 아니다.
어휘 수가 늘어나면 감당할 수 없기 때문이다.
따라서 근사적인 해법으로, 부정적 예를 몇개 샘플링한다. 이것이 네거티브 샘플링이다.
정리하면, 긍정적 예를 target으로 한 경우의 손실을 구한다.
그와 동시에 부정적 예를 몇개 샘플링 하여, 마찬가지로 손실을 구한다.
그리고 각각의 손실을더한 값을 최종 손실로 한다.
부정적 예의 타깃을 2개 샘플링했다고 가정한다. 계산그래프는 아래와 같이 그릴 수 있다.

네거티브 샘플링의 샘플링 기법
부정적 예를 어덯게 샘플링하느냐인데, 무작위 샘플링하는 것보다 좋은 방법이 있다.
말뭉치의 통계 데이터를 기초로 샘플링하는 방법이다.
구체적으로는, 말뭉치에서 자주 등장하는 단어를 많이 추출하고 드물게 등장하는 단어를 적게 추출하는 것이다.
말뭉치에서의 단어 빈도를 기준으로 샘플링하려면, 먼저 말뭉치에서 각 단어의 출현 횟수를 구해 확률분포로 나타낸다.
그 다음 확률분포대로 단어를 샘플링하면 된다.

네거티브 샘플링에서는 부정적 예를 가능한 많이 다루는 것이 좋지만, 계산량 문제 때문에 적은 수(5개, 10개 등)로 한정해야 한다. 그런데 우연히 희소한 단어들만 선택되었다면? 결과도 당연히 나빠진다.
드문 단어를 잘 처리하는 일은 중요도가 낮다. 흔한 단어를 잘 처리하는 것이 좋은 결과로 이어질 것이다.
확률 분포에 따라 샘플링하는 예를 파이썬 코드로 작성해보자.
#0에서 9까지의 숫자 중 하나를 무작위로 샘플링
np.random.choice(10)
np.random.choice(10)
#words에서 하나만 무작위로 샘플링
words = ['you','say','goodbye','I','hello','.']
np.random.choice(words)
#5개만 무작위로 샘플링(중복 있음)
np.random.choice(words,size = 5)
# '' (중복 없음)
np.random.choice(words, size = 5, replace = False)
#확률분포에 따라 샘플링
p = [0.5,0.1,0.05,0.2,0.05,0.1]
np.random.choice(words, p = p)word2vec의 네거티브 샘플링에서는 앞의 확률분포에서 한가지를 수정하라고 권고하고 있다.
아래 식처럼 기본 확률분포에 0.75를 제곱하는 것이다.

수정 후에도 총합은 1이 되어야 하므로, 분모로는 수정 후 확률분포의 총합이 필요하다.
그럼 위 식처럼 수정하는 이유는 뭘까? 출현 확률이 낮은 단어를 버리지 않기 위해서이다.
더 정확히 말하자면, 출현 확률이 낮은 단어의 확률을 보정하는 것이다.
예를 보자.
p =[0.7,0.29,0.01]
new_p = np.power(p,0.75)
new_p /= np.sum(new_p)
print(new_p)
수정 전 확률이 0.01이던 원소가 보정 후에는 0.0265...로 높아졌다.
지금까지 본 내용처럼 네거티브 샘플링은 말뭉치에서 단어의 확률분포를 만들고, 다시 0.75제곱을 해준 뒤, 부정적 예를 샘플링한다. 이 책에서는 처리를 담당하는 클래스 UnigramSampler를 제공한다.
UnigramSampler는 초기화시 3개의 인수를 받는다. 단어 ID 목록 corpus, 확률분포 제곱값 power(기본값 0.75), 부정적 예 샘플링 수행횟수 sample_size이다.
이 클래스에서 get_negative_samplge(target)메서드를 제공한다. target을 긍정적 예의 단어로 해석하고, 그 이외의 단어 ID를 샘플링(부정적 예)한다. 예를 보자.
from negative_sampling_layer import UnigramSampler
corpus = np.array([0,1,2,3,4,1,2,3])
power = 0.75
sample_size = 2
sampler = UnigramSampler(corpus,power,sample_size)
target = np.array([1,3,0])
negative_sample = sampler.get_negative_sample(target)
print(negative_sample)
이 예시에서는 긍정적 예로 [1, 3, 0]이라는 3개의 데이터를 미니배치로 다뤘다.
각각의 데이터에 대해 부정적 예를 2개씩 샘플링한다.
네거티브 샘플링 구현
네거티브 샘플링 구현 코드이다. 우선 초기화 메서드를 보자.
class NegativeSamplingLoss:
def __init__(self, W, corpus, power=0.75, sample_size=5):
self.sample_size = sample_size
self.sampler = UnigramSampler(corpus, power, sample_size)
self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]
self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]
self.params, self.grads = [], []
for layer in self.embed_dot_layers:
self.params += layer.params
self.grads += layer.grads출력측 가중치 W, 말뭉치(단어 ID 리스트)를 뜻하는 corpus, power, 부정적 예의 샘플링 횟수 sample_size가 있다.
앞 절에서 설명한 UnigramSampler를 생성하여 sampler로 저장한다. 부정적 예 샘플링 횟수도 sample_size에 저장한다.
인스턴스 변수 loss_layers와 embed_dot_layers에서는 원하는 계층을 리스트로 보관한다.
이어서 순전파의 구현을 보자.
def forward(self, h, target):
batch_size = target.shape[0]
negative_sample = self.sampler.get_negative_sample(target)
# 긍정적 예 순전파
score = self.embed_dot_layers[0].forward(h, target)
correct_label = np.ones(batch_size, dtype=np.int32)
loss = self.loss_layers[0].forward(score, correct_label)
# 부정적 예 순전파
negative_label = np.zeros(batch_size, dtype=np.int32)
for i in range(self.sample_size):
negative_target = negative_sample[:, i]
score = self.embed_dot_layers[1 + i].forward(h, negative_target)
loss += self.loss_layers[1 + i].forward(score, negative_label)
return loss이 메서드가 받는 인수는 은닉층 h와 긍정적 예 target이다.
우선 self.sampler를 이용해 부정적 예를 샘플링하여 negative_sample에 저장한다.
그다음 긍정적,부정적 예 각각의 데이터에 대해 순전파를 수행해 그 손실을 더한다.
구체적으로는 Embedding Dot계층의 forward 점수를 구하고, 이어서 이 점수와 레이블을 Sigmoid with Loss 계층으로 흘려 손실을 구한다. correct_label은 정답 레이블은 1, 오답 레이블은 0임에 주의하자.
마지막으로 역전파 구현 코드를 보자.
def backward(self, dout=1):
dh = 0
for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
dscore = l0.backward(dout)
dh += l1.backward(dscore)
return dh역전파는 간단하다. 순전파 때의 역순으로 각 계층의 backward()를 호출하기만 하면 된다.
은닉층의 뉴런은 순전파 시에 여러개로 복사되었다. 이전의 절에서 설명한 Repeat노드에 해당한다.
따라서 역전파 때에는 여러개의 기울기 값을 더해준다.
개선판 word2vec 학습
Embedding계층과 네거티브 샘플링 기법의 개선을 신경망 구현에 적용해보자.
그 PTB데이터셋을 사용해 학습하고 더 실용적인 단어의 분산 표현을 얻어보자.
CBOW 모델 구현
CBOW 모델을 구현할 건데, 앞 장의 단순한 SimpleCBOW를 개선하고 맥락의 윈도우 크기를 임의로 조절할 수 있도록 확장한다.
# -*- coding: utf-8 -*-
"""
Created on Tue Dec 24 15:11:48 2024
Created by SeungKeon Lee
"""
import sys
from negative_sampling_layer import NegativeSamplingLoss
sys.path.append('..')
import numpy as np
from common.layers import Embedding
class CBOW:
def __init__(self,vocab_size,hidden_size,window_size,corpus):
V, H = vocab_size, hidden_size
#가중치 초기화
W_in = 0.01 * np.random.randn(V,H).astype('f')
W_out = 0.01 * np.random.randn(V,H).astype('f')
#layer 생성
self.in_layers = []
for i in range(2 * window_size):
layer = Embedding(W_in) #Embedding 계층 사용
self.in_layers.append(layer)
self.ns_loss = NegativeSamplingLoss(W_out, corpus,power = 0.75,sample_size = 5)
#모든 가중치와 기울기를 배열에 모은다
layers = self.in_layers + [self.ns_loss]
self.params, self.grads = [], []
for layer in layers:
self.params += layer.params
self.grads += layer.grads
#인스턴스 변수에 단어의 분산 표현을 저장한다.
self.word_vecs = W_in초기화 메서드에서 어휘수,은닉층 뉴런수, 단어 ID 목록, 맥락의 크기를 지정한다.
가중치 초기화가 끝나면, 계층을 생성한다. Embedding 계층을 2 * window_size로 작성하여 in_layers에 배열로 저장한다.
그 다음 Negative Sampling Loss 계층을 생성한다.
이후 이 신경망에서 사용하는 모든 매개변수와 기울기를 인스턴스 변수인 params와 grads에 모은다.
또한 나중에 단어의 분산 표현에 접근할 수 있도록 인스턴스 변수인 word_vecs에 가중치 W_in을 할당한다.
순전파 역전파 메서드를 보자.
def forward(self,contexts,target):
h = 0
for i,layer in enumerate(self.in_layers):
h += layer.forward(contexts[:,i])
loss = self.ns_loss.forward(h, target)
return loss
def backward(self,dout = 1):
dout = self.ns_loss.backward()
dout *= 1 / len(self.in_layers)
for layer in self.in_layers:
layer.backward(dout)
return None이 구현은 계층의 순전파,역전파를 적절한 순서로 호출한 것이다.
forward에서 (contexts,target)메서드가 인수로 받는 것이 단어 ID라는 점이 개선점이다. 아래 그림을 참고하자.

오른쪽에 보이는 단어 ID의 배열이 contexts와 target의 예이다.
CBOW 모델 학습 코드
CBOW 모델 학습을 구현해보자. 여기서는 단순히 신경망 학습을 수행할 뿐이다.
# -*- coding: utf-8 -*-
"""
Created on Tue Dec 24 15:34:30 2024
Created by SeungKeon Lee
"""
import sys
sys.path.append('..')
import numpy as np
from common import config
# =============================================================================
#
# config.GPU = True
# =============================================================================
import pickle
from common.trainer import Trainer
from common.optimizer import Adam
from cbow import CBOW
from common.util import create_contexts_target, to_cpu, to_gpu
from dataset import ptb
#하이퍼파라미터 설정
window_size = 5
hidden_size= 100
batch_size = 100
max_epoch = 10
#data 읽기
corpus,word_to_id,id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
if config.GPU:
contexts, target = to_gpu(contexts), to_gpu(target)
#모델 등 생성
model = CBOW(vocab_size, hidden_size, window_size, corpus)
optimizer = Adam()
trainer = Trainer(model, optimizer)
#학습 시작
trainer.fit(contexts,target,max_epoch, batch_size)
trainer.plot()
#나중에 사용할 수 있도록 필요한 데이터 저장
word_vecs = model.word_vecs
if config.GPU:
word_vecs = to_cpu(word_vecs)
params = {}
params['word_vecs'] = word_vecs.astype(np.float16)
params['word_to_id'] = word_to_id
params['id_to_word'] = id_to_word
pkl_file = 'cbow_params.pkl'
with open(pkl_file,'wb') as f:
pickle.dump(params, f,-1)이번 CBOW모델은 윈도우 크기를 5로, 은닉층의 뉴런 수를 100개로 설정했다.
사용하는 말뭉치에 따라 다르지만, 윈도우 크기는 2~10개, 은닉층의 뉴런 수(단어의 분산 표현의 차원 수)는 50~500개 정도면 좋은 결과를 얻을 것이다.


CBOW 모델 평가
학습한 단어의 분산 표현을 평가해보자. 2장에서 구현한 most_similar()메서드를 이용하여 단어 몇개에 대해 거리가 가장 가까운 단어들을 뽑아보자.
# -*- coding: utf-8 -*-
"""
Created on Tue Dec 24 17:51:26 2024
Created by SeungKeon Lee
"""
import sys
sys.path.append('..')
from common.util import most_similar
import pickle
pkl_file = 'cbow_params.pkl'
with open(pkl_file,'rb') as f:
params = pickle.load(f)
word_vecs = params['word_vecs']
word_to_id = params['word_to_id']
id_to_word = params['id_to_word']
querys = ['you', 'year', 'car', 'toyota']
for query in querys:
most_similar(query, word_to_id, id_to_word, word_vecs,top=5)

word2vec으로 얻은 단어의 분산 표현은 비슷한 단어를 가까이 모을 뿐 아니라, 더 복잡한 패턴을 파악하는 것으로 알려져 있다.
대표적인 예가 "king - man + woman = queen"으로 유명한 유추 문제(비유 문제)이다.
정확하게 말하면, word2vec의 단어 분산 표현을 사용하면 유추 문제를 벡터의 덧셈과 뺄셈으로 풀 수 있다는 뜻이다.
실제로 유추 문제를 풀려면 아래 그림처럼 단어 벡터 공간에서 "man -> woman"벡터와 "king -> ?" 벡터가 가능한 한 가까워지는 단어를 찾는다.

man의 분산 표현(단어 벡터)를 vec('man')이라고 표현해보자.
그러면 위의 관계를 수식으로 나타내면 vec('woman') - vec('man') = vec(?) - vec('king')이 된다.
common/util.py의analogy()를 이용해보자.
analogy('man', 'king', 'woman', word_to_id, id_to_word, word_vecs, top = 5)
위처럼 word2vec으로 얻은 단어의 분산 표현을 사용하면, 벡터의 덧셈과 뺄셈으로 유추 문제를 풀 수 있다.
word2vec 남은 주제
word2vec을 사용한 애플리케이션의 예
word2vec으로 얻은 단어의 분산 표현은 비슷한 단어를 찾는 용도로 이용할 수 있다.
그러나 단어 분산 표현의 장점은 여기서 끝이 아니다.
자연어 처리 분야에서 단어의 분산 표현이 중요한 이유는 전이 학습(transfer learning)에 있다.
전이 학습은 한 분야에서 배운 지식을 다른 분야에도 적용하는 기법이다.
자연어 문제를 풀 때 word2vec의 단어 분산 표현을 처음부터 학습하는 일은 거의 없다.
그 대신 먼저 큰 말뭉치(위키백과, 구글 뉴스의 텍스트 데이터 등)로 학습을 끝낸 후, 분산 표현을 각자의 작업에 이용하는 것이다.
단어의 분산 표현은 단어를 고정 길이 벡터로 변환해준다는 장점도 있다.
문장(단어의 흐름)도 단어의 분산 표현을 사용하여 고정 길이 벡터로 변환할 수 있다.
위 방법중 가장 간단한 방법은 bag-of-words라 하며, 단어의 순서를 고려하지 않는 모델이다.
다음 장에서 설명하는 순환 신경망(RNN)을 사용하면 한층 세련된 방법으로 (word2vec의 단어 분산 표현을 이용하며) 문장을 고정 길이 벡터로 변환할 수 있다.
단어나 문장을 고정 길이 벡터로 변환할 수 있다는 점은 매우 중요하다.
자연어를 벡터로 변환할 수 있다면 일반적인 머신러닝 기법(신경망이나 SVM 등)을 적용할 수 있기 때문이다.
다음 그림을 참고하자.

위 그림의 파이프라인에서는 단어의 분산 표현 학습과 머신러닝 시스템의 학습은 서로 다른 데이터셋을 사용해 개별적으로 수행하는 것이 일반적이다.
단어의 분산 표현은 위키백과와 같은 범용 말뭉치를 사용해 미리 학습해둔다. 그리고 현재 직면한 문제에 관련하여 수집한 데이터를 가지고 머신러닝 시스템을 학습시킨다.
다만, 직면한 문제의 학습 데이터가 아주 많다면 단어의 분산 표현과 머신러닝 시스템 학습 모두를 처음부터 수행하는 방안도 고려해볼 수 있다.
구체적인 예를 보자. 사용자가 1억명 이상인 스마트폰 앱을 운영하고 있다고 해보자.
받은 메일을 자동으로 분류하는 시스템을 만들 고민을 한다. 사용자의 감정을 정확하게 분류할 수 있다면, 불만을 가진 사용자의 메일부터 순서대로 살펴볼 수 있다.
그렇게 된다면 앱의 치명적인 문제를 조기에 발견하고 손을 쓸 수 있고, 사용자의 만족감도 높아질 것이다.

메일 자동 분류 시스템을 만드려면, 우선 데이터(메일)을 수집해야 한다.
지금 예에서는 사용자가 보낸 메일들에 수동으로 레이블을 붙인다. 3단계 감정을 나타내는 레이블(긍정적 positive, 중립적 neutral, 부정적 negative)을 붙인다.
레이블링 작업이 끝나면 학습된 word2vec을 이용해 메일을 벡터로 변환한다.
그 다음 감정 분석을 수행하는 어떤 분류 시스템(SVM이나 신경망 등)에 벡터화된 메일과 감정 레이블을 입력하여 학습을 수행한다.
위 예처럼 자연어를 다루는 문제는 단어의 분산 표현이라는 방법으로 벡터화할 수 있다. 그 덕분에 일반적인 머신러닝 기법으로 해결할 수 있게 되는 것이다.
단어 벡터 평가 방법
단어의 분산 표현은 앞 절에서 본 감정 분석 예처럼, 현실적으로는 특정한 애플리케이션에서 사용되는 것이 대부분이다.
그렇다면 우리가 궁극적으로 원하는 것은 정확도 높은 여러 시스템이다.
단어의 분산 표현을 만드는 시스템과 분류하는 시스템의 학습은 따로 수행할 수도 있다.
그 경우, 단어의 분산 표현의 차원 수가 최종 정확도에 어떤 영향을 주는지를 조사하려면, 우선 단어의 분산 표현을 학습하고 그 분산 표현을 사용하여 또 하나의 머신러닝 시스템을 학습시켜야 한다.
두단계의 학습을 수행한 다음 평가해야 할 것이다. 이 경우 두 시스템 각각에서 최적의 하이퍼파라미터를 찾기 위한 튜닝도 필요하므로, 그만큼 시간이 오래 걸린다.
그래서 단어의 분산 표현의 우수성을 실제 애플리케이션과는 분리해 평가하는 것이 일반적이다.
이때 자주 사용되는 평가 척도가 단어의 1) 유사성이나 2) 유추 문제를 활용한 평가이다.
1) 유사성 평가에서는 사람이 작성한 단어 유사도를 검증 세트를 사용해 평가하는 것이 일반적이다.
예를 들어 유사도를 0~10사이로 점수화한다면 cat과 animal의 유사도는 8, cat과 car의 유사도는 2와 같이 사람이 단어 사이의 유사한 정도를 규정한다.
그리고 사람이 부여한 점수와 word2vec에 의한 코사인 유사도 점수를 비교해 그 상관성을 보는 것이다.
2) 유추 문제를 활용한 평가는 king : queen = man : ? 와 같은 유추 문제를 출제하고, 그 정답률로 단어의 분산 표현의 우수성을 측정한다. 아래 그림은 논문에서 유추 문제에 의한 평가가 실려 있는 부분을 일부 발췌한 것이다.

word2vec 모델, 단어 분산 표현의 차원 수, 말뭉치 크기를 매개변수로 사용해 실험을 수행한 결과이다.
semantics(의미) 열은 단어의 의미를 유추하는 유추 문제의 정답률을 보여준다.
king : queen = actor : actress와 같이 단어의 의미를 묻는 문제이다.
syntax(구문) 열은 단어의 형태 정보를 묻는 문제로 bad : worst = good : best같은 문제를 말한다.
위 결과로부터 다음 사항을 알 수 있다.
- 모델에 따라 정확도가 다르다.(말뭉치에 따라 적합한 모델 선택)
- 일반적으로 말뭉치가 클수록 결과가 좋다.(데이터는 다다익선)
- 단어 벡터 차원은 적당한 크기가 좋다.(차원이 너무 커도 정확도가 나빠짐)
유추 문제를 이용하면 단어의 의미나 문법적인 문제를 제대로 이해하고 있는지를 어느정도 측정할 수 있다.
다만, 단어의 분산 표현의 우수함이 애플리케이션에 얼마나 기여하는지는 애플리케이션 종류나 말뭉치의 내용 등, 다루는 문제 상황에 따라 다르다.
즉, 유추 문제에 의한 평가가 높다고 해서 해당 애플리케이션도 반드시 좋은 결과가 나오리라는 보장은 없다.
정리
- Embedding 계층은 단어의 분산 표현을 담고 있으며, 순전파시 지정한 단어 ID의 벡터를 추출한다.
- word2vec은 어휘 수 증가에 비례하여 계산량도 증가하므로, 근사치로 계산하는 빠른 기법을 사용하면 좋다.
- 네거티브 샘플링은 부정적 예 몇개를 샘플링하는 기법으로, 이를 이용하면 다중 분류를 이진 분류처럼 취급할 수 있다.
- word2vec으로 얻은 단어의 분산 표현에는 단어의 의미가 녹아들어 있으며, 비슷한 맥락에서 사용되는 단어는 단어 벡터 공간에서 가까이 위치한다.
- wod2vec의 단어 분산 표현을 이용하면 유추 문제를 덧셈과 뺄셈으로 풀 수 있게 된다.
- word2vec은 전이 학습 측면에서 특히 중요하며, 그 단어의 분산 표현은 다양한 자연어 처리 작업에 이용할 수 있다.
'공부 > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝2 - Chap6. 게이트가 추가된 RNN (2) | 2025.01.01 |
|---|---|
| 밑바닥부터 시작하는 딥러닝2 - Chap5. 순환 신경망(RNN) (2) | 2024.12.27 |
| 밑바닥부터 시작하는 딥러닝2 - Chap3. word2vec (3) | 2024.12.23 |
| 밑바닥부터 시작하는 딥러닝2 - Chap2. 자연어와 단어의 분산 표현 (4) | 2024.12.16 |
| 밑바닥부터 시작하는 딥러닝2 - Chap1. 신경망 복습 (3) | 2024.12.14 |